Introductory material

Introductory material#

EDRIXS is an open-source toolkit for performing exact diagonalization RIXS calculations. See Ref. [1] for the original paper, Ref. [2] for the docs, and Ref. [3] for the source code.

Geometry and notation#

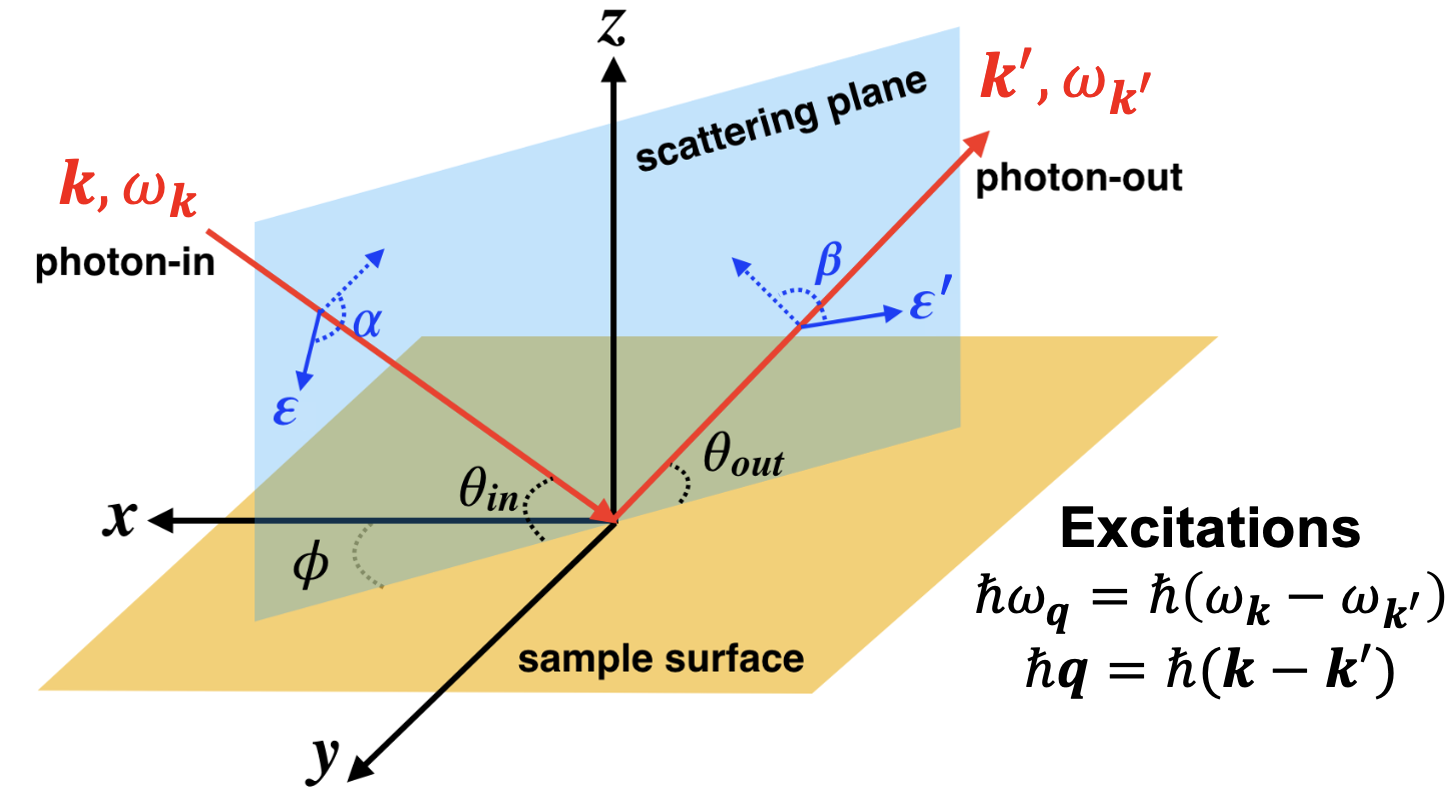
Consider a typical setup for RIXS. Setup for RIXS

Here, RIXS intensity is described by [4]

\[\begin{split} I \propto \frac{1}{\mathcal{Z}(T)}\sum_{i}e^{- E_{i}/(k_\mathrm{B}T)} \\ \times \sum_f |M_{fi}|^2 \delta(E_f + \hbar\omega_{\boldsymbol{k}^\prime} - E_i - \hbar\omega_{\boldsymbol{k}} ) \end{split}\]

where \(\mathcal{Z}(T) = \sum_i e^{- E_i/(k_\mathrm{B}T)}\) is the partition function. The main part of the physics is in the matrix elements \(M_{fi}\), which can be illustrated as

Matrix elements

and calculated via

\[ M_{fi} = \sum_n \frac{\bra{f} {\cal D}^\dagger_{\boldsymbol{k}^\prime\hat{\epsilon}^\prime}\ket{n}\bra{n} {\cal D}^{\phantom\dagger}_{\boldsymbol{k}\hat{\epsilon}}\ket{i}}{E_n - E_i - \hbar\omega_{\boldsymbol{k}}+\mathrm{i}\Gamma_n/2}. \]

Hamiltonian#

Adopting the second quantization formalism, Hamiltonians in EDRIXS involve:

A two fermion term that accounts for:

  • Crystal field. For example \(10 D_q\), which is the splitting between the \(e_g\) and \(t_{2g}\) orbitals in octahedral symmetry.

  • Spin orbit coupling, \(\lambda_i\), \(\lambda_n\), \(\lambda_c\)

  • Hopping (in cases where this is part of the model) \(V_{eg}\), \(V_{t2g}\)

  • Charge-transfer energy \(\Delta\)

The four fermion term that accounts for:

  • Intra-valence-shell Coulomb interactions e.g. Slater integrals \(F^0_{dd,i}\), \(F^2_{dd,i}\), and \(F^4_{dd,i}\) for a \(d\) shell.

  • Core-valence Coulomb interactions e.g. Slater integrals \(G^1_{dp}\) and \(G^3_{dp}\) for \(L\)-edge RIXS.

Contents